Les cadrans de hauteur à lignes horaires rectilignes

Yvon MASSE

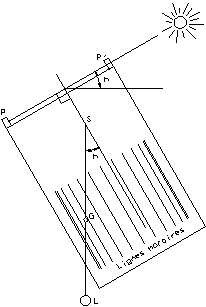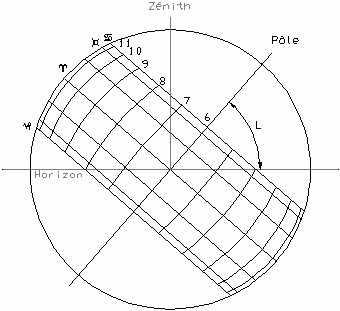
Fig. 1 Ces cadrans sont constitués d'une table comprenant:

Des lignes horaires parallèles et rectilignes
Deux pinnules P et P' dont l'axe de visée est perpendiculaire aux lignes horaires
Le principe de l'utilisation de ces cadrans consiste à laisser pendre, d'un point S défini pour la date et éventuellement la latitude du lieu de l'observation, un fil muni d'un lest L et d'une perle coulissante G. La distance de S à G est à régler avant l'observation. Quand la table du cadran est verticale et le soleil dans l'alignement des pinnules, la position de G sur les lignes horaires donne l'heure solaire.
Remarquons tout de suite que, lorsque le cadran pointe ainsi l'astre du jour, la hauteur du soleil au-dessus de l'horizon se retrouve, par définition, entre le fil et la direction des lignes horaires.

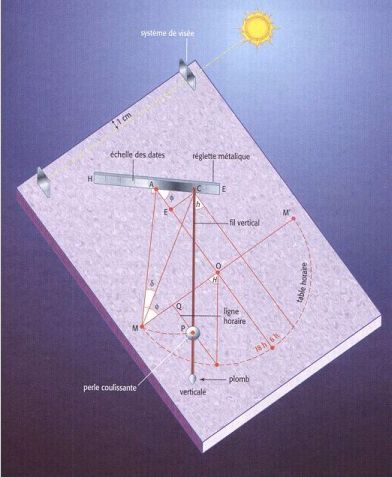
Fig.1: Cadran de hauteur à lignes horaires rectilignes

Les plus anciennes réalisations connues de ce type de cadran remontent au XIV° siècle et se présentent sous la forme d'un navire auquel on a donné le nom de Navicula de venetiis. Ce cadran est Universel car il peut être réglé pour fonctionner sous différentes latitudes mais il ne donne pas rigoureusement l'heure solaire à moins d'introduire, après lecture, une correction en fonction de la déclinaison du soleil et de l'heure lue.

C'est Regiomontanus, astronome Allemand, qui donna vers 1474, sans doute à partir d'écrits plus anciens mais inconnus à ce jour, la première description mathématiquement juste d'un cadran assez similaire à la Navicula de venetiis et auquel on a donné le nom d'Universel de Regiomontanus (Fig. 2).

Au début des années 1530 apparu (ou réapparu ?) la description d'un autre cadran de ce type mais ne fonctionnant que pour une latitude donnée, on lui donna le nom de Capucin en raison de la ressemblance des lignes horaires, limitées à leur partie utile par deux arcs de cercle, au capuchon d'un moine (Fig. 3).

Un autre type de cadran universel dérivant du Capucin fut décrit en 1533 par Peter Apian dans son livre Instrument Buch. Par les mystères de l'histoire ce cadran resta quelque peu oublié.

Il fallut attendre jusqu'en 1674 pour que Millet Deschalles donne une démonstration par la géométrie du principe de l'Universel de Regiomontanus, démonstration par ailleurs assez complexe.

Fig. 2 Fig. 3
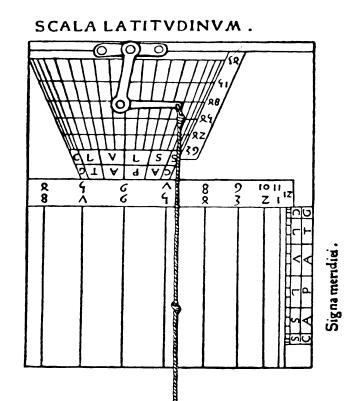
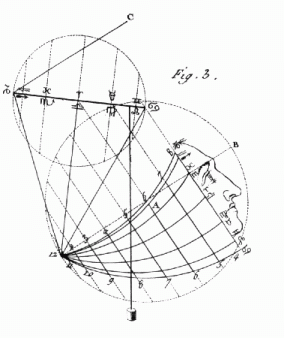
Fig. 2: L'Universel de Régiomontanus. Le fil est suspendu à l'intersection des lignes horizontales de latitude et des lignes inclinées de déclinaison. En tirant sur le fil, on règle la perle, ou ici le noeud, sur l'échelle latérale des déclinaisons. Fig. 3: Le Capucin. Le point de suspension du fil se règle sur une échelle de date. La perle qui doit se régler sur le point 12 est remplacée ici par un ensemble d'arcs de cercle.

En 1819, dans son Histoire de l'astronomie du moyen âge, Delambre voit dans la complexité de cette démonstration ainsi que dans son absence des traités plus anciens la preuve que l'invention de ce cadran soit "étrangère à l'Europe et nous ne voyons que les Arabes à qui nous puissions en faire l'honneur". Il donne alors sa propre démonstration par la trigonométrie plane ce qui sera pour longtemps le seul moyen utilisé par d'autres auteurs pour expliquer la validité de ce cadran.

Dans une publication de 1957, A. W. Fuller s'efforça de donner une démonstration géométrique simple pour retrouver le cheminement parcouru par les inventeurs de l'Universel de Regiomontanus. Il avança une hypothèse intéressante voyant dans le fil lesté avec sa perle le rayon d'un cercle et dans la table du cadran les différentes positions de son centre.

C'est cette hypothèse que nous allons exploiter dans la démonstration suivante mais, à l'inverse de Fuller et bien que partant de ses données initiales, nous expliquerons non pas l'Universel de Regiomontanus mais le Capucin puis l'Universel d'Apian. Ensuite, en partant d'un point de vue différent, nous aboutirons par un raisonnement similaire à l'Universel de Regiomontanus. Pour terminer, ajoutons que les démonstrations proposées se veulent avant tout explicites, quitte à sacrifier si nécessaire à la rigueur mathématique.

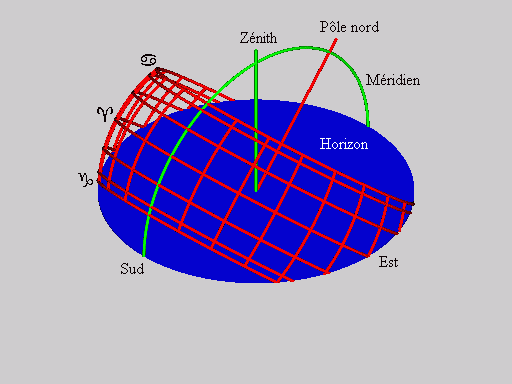Fig. 4 La figure 4 montre la sphère céleste pour une latitude donnée telle qu'on a l'habitude de l'imaginer en gnomonique.
Fig. 4: La sphère céleste avec ses cercles horaires et de déclinaison

En projetant tous les cercles de la sphère perpendiculairement sur le plan du méridien on obtient la figure 5 encore appelée Analemme de Ptolémée. L'analemme doit être disposé en fonction de la latitude, puis, de la déclinaison et de l'heure solaire, on peut déterminer la position du soleil pour finalement déterminer sa hauteur au dessus de l'horizon. Fig. 5
Fig. 5: L'analemme de Ptolémée. Le méridien devient le grand cercle principal, les cercles de déclinaison deviennent des segments de droite et les cercles horaires deviennent des portions d’ellipse.

Décomposons sur la figure 6 toutes les étapes conduisant à obtenir la hauteur du soleil en fonction de:

La latitude L
La déclinaison du soleil
Son angle horaire Ah

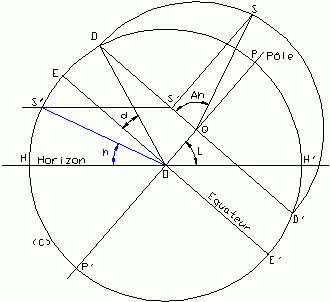Du centre O traçons le cercle (C) correspondant au méridien
Par O traçons l'horizon HH'
Par O traçons l'axe des pôles PP' faisant avec l'horizon l'angle L de la latitude
Perpendiculairement à l'axe des pôles traçons l'équateur EE'
Traçons le rayon OD faisant avec l'équateur l'angle de déclinaison du soleil d
Traçons parallèlement à l'équateur la corde DD' correspondante à la trace du cercle de déclinaison
Du centre Q traçons le demi-cercle DSD' correspondant au rabattement du cercle de déclinaison
Traçons le rayon QS faisant avec QD l'angle horaire Ah du soleil
Abaissons S perpendiculairement à DD' pour obtenir la position du soleil S'
Reportons la distance de S' à l'horizon sur le cercle en traçant l'horizontale S'S"
Traçons le rayon OS". L'angle de la hauteur du soleil correspond à HOS"

Fig. 6

Cela faisant nous avons en grande partie tracé les lignes du Capucin. En effet, complétons la figure en traçant les horizontales S'S" correspondantes à toutes les heures solaires entières et, pour retrouver une orientation plus familière, faisons tourner l'ensemble de 90°. Nous obtenons la figure 7 sur laquelle on peut associer:

Au point O le point de suspension du fil
Au Point S" la perle coulissante
Aux différentes horizontales (maintenant verticales) les lignes horaires rectilignes qui sont écartées de la ligne de 6 h proportionnellement au cosinus de Ah
Pour faire l'inverse, c'est-à-dire à partir des lignes horaires rectilignes retrouver le centre et le rayon du cercle méridien, il faut, à partir du point Q situé sur la ligne centrale de 6 h:

Tracer, en fonction de la latitude et perpendiculairement entre eux, l'axe des pôles PP' ainsi que la droite QD, D étant situé sur la ligne horaire de 12 h
De D, en fonction de la déclinaison du soleil, tracer la droite DO donnant le centre O et le rayon OD
Fig. 7
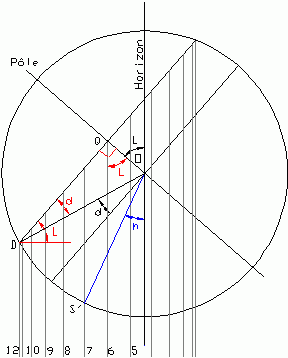Fig. 7

C'est de ce centre qu'il faut suspendre le fil lesté et, avant d'utiliser le cadran, aligner le fil sur la droite OD et régler la perle coulissante sur le point D.

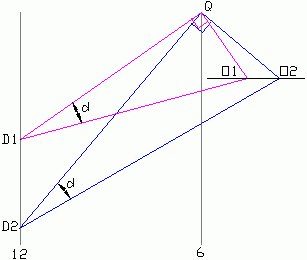
Fig. 8 Fig. 9
Fig. 8 Fig. 9: Le capucin. On peut reconnaître dans l'échelle des dates l'axe des pôles, dans le point C le centre du cercle méridien, dans la longueur MC son rayon et dans le segment AM la trace du cercle de déclinaison (figure extraite du livre Les Cadrans Solaires de D. Savoie).
Fig. 10 En répétant l'opération précédente pour plusieurs latitudes, le passage à l'Universel d'Apian vient alors naturellement. Mais regardons d'abord sur la figure 8 ce qui se passe pour seulement 2 latitudes.
Du point Q et pour la latitude L1, retrouvons le centre O1 du cercle méridien à l'aide du triangle QD1O1. De même pour la latitude L2 traçons le triangle QD2O2 pour obtenir le centre O2. Intéressons nous à présent au triangle QD1D2 et remarquons que:

L'angle O1QO2 est égal à l'angle D1QD2
Les triangles QD1O1 et QD2O2 sont semblables donc QO1 est à QD1 ce que QO2 est à QD2
Par conséquent les triangles QD1D2 et QO1O2 sont donc semblables et comme la similitude est directe et d'angle droit, la droite O1O2 est donc perpendiculaire à la ligne de midi. Par extension, tous les centres O que nous obtiendrons pour des latitudes différentes mais pour la même déclinaison d seront situés sur cette droite.
Nous pouvons à présent mieux comprendre la forme de l'Universel d'Apian présenté à la figure 10.

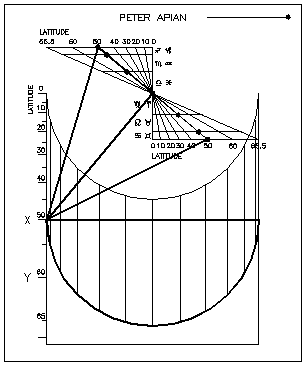
Fig. 10: L'Universel d’Apian. Le point de fixation du fil est dans le "papillon" supérieur à l'intersection des lignes inclinées de latitude (image des différents axes polaires) et des lignes horizontales de déclinaison. La perle se règle sur l'échelle latérale des latitudes (figure de Fer J. de Vries).

Comparons maintenant les Universels d'Apian et de Regiomontanus (fig. 2) en s'intéressant au différentes échelles qui permettent de définir le point de fixation du fil et la position de la perle.

Echelle latérale Lignes obliques Lignes horizontales
Universel d'Apian Latitude Latitude Déclinaison
Universel de Regiomontanus Déclinaison Déclinaison Latitude

	Echelle latérale	Lignes obliques	Lignes horizontales
Universel d'Apian	Latitude	Latitude	Déclinaison
Universel de Regiomontanus	Déclinaison	Déclinaison	Latitude

Il apparaît nettement qu'il existe une dualité entre la déclinaison et la latitude. On peut par ailleurs retrouver cette dualité dans la formule de la hauteur h du soleil qui s'écrit:

sin h = sin d.sin L + cos d.cos L.cos Ah

Dans cette formule, la déclinaison et la latitude sont utilisées aux mêmes endroits et avec les mêmes fonctions trigonométriques. On peut donc remplacer la déclinaison par la latitude et inversement ce qui nous permettrait de passer naturellement de l'Universel d'Apian à celui de Regiomontanus. Mais préférons l’approche géométrique suivante, similaire à la première mais partant d’un autre point de vue: nous avons considéré le soleil vu de la terre, considérons à présent la terre vue du soleil.

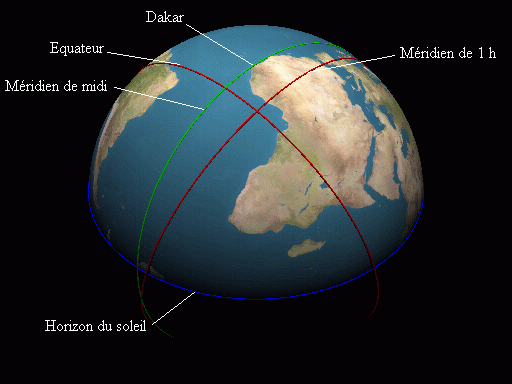Fig. 11 Sur la figure 11, le pied du soleil est au Sénégal près de Dakar. Là, la hauteur du soleil est de 90°. Par Dakar passe le méridien vert, en tout lieu sur ce méridien il est midi vrai. 15° à l'ouest passe le méridien rouge, en tout lieu sur ce dernier il est 1 heure vraie.
Fig. 11: La terre éclairée par le soleil

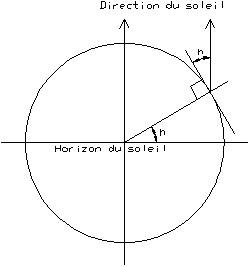Le cercle bleu appelé horizon du soleil sépare le monde de la lumière de celui des ténèbres. En tout lieu sur ce cercle, le soleil est vu sur l’horizon. Comme le montre la figure 12, en tout point du monde éclairé, l’angle de la hauteur du soleil correspond à l’angle, vu du centre de la terre, du lieu considéré au plan de l’horizon du soleil. Fig. 12
Fig. 12: Vue en coupe de la terre. La coupe passe par le pied du soleil et le lieu considéré.

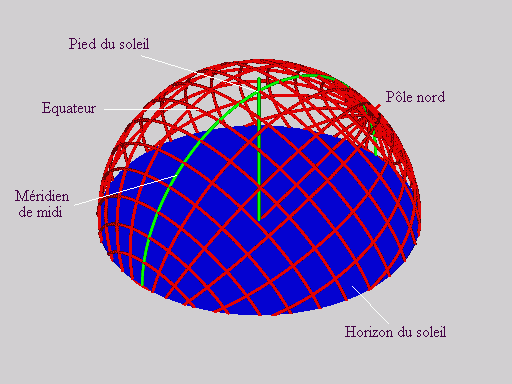Représentons à présent, figure 13, la terre par tous ses cercles parallèles et méridiens. Ces derniers, régulièrement espacés tous les 15 °, peuvent être gradués en heure solaire comme nous l'avons vu ci-dessus. Convenons alors d'appeler angle horaire terrestre l'angle qui sépare un méridien donné du méridien de midi. Fig. 13
Fig. 13: La terre avec tous ses parallèles et méridiens

Projetons maintenant tous les cercles perpendiculairement sur le plan du méridien de midi, nous obtenons la figure 14.

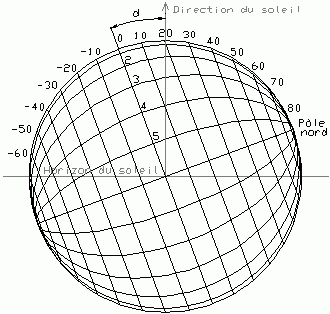Fig. 14 Cette projection, équivalente à l'analemme de Ptolémée, doit être disposée en fonction de la déclinaison du soleil. On peut alors voir d'un coup d'oeil la durée du jour et de la nuit en fonction du parrallèle où l'on se situe. Suivant l'heure solaire, à laquelle on fait correspondre un méridien, on peut retrouver l'angle de hauteur du soleil.
Pour retrouver l'analemme de Ptolémée il suffit de remplacer l'angle de la déclinaison par celui de la latitude et les segments des parallèles par ceux des déclinaisons. En récapitulant, ce que nous avons proposé au départ comme une astuce mathématique (la permutation de L et d) prend ici une réalité physique et bien que ce point de vue ne soit pas familier au gnomoniste il n'était pas ignoré des cartographes, au moins depuis Ptolémée qui avait découpé le monde en latitudes et longitudes.

Fig. 14: Le méridien de midi est le grand cercle principal. Les cercles des parallèles deviennent des segments de droite. d est la déclinaison du soleil.

N'en doutons plus maintenant, à partir de ce point de vue et en reprenant les étapes de la démonstration précédente nous aboutirons avec la même facilité à l'Universel de Regiomontanus en passant par un cadran particulier, n'ayant à vrai dire peu d'intérêt, qui donne l'heure, pour une déclinaison particulière, en fonction de la latitude.

Retraçons pour le plaisir les figures 15 et 16 qui nous donneront les différents angles à utiliser pour la construction de l'Universel de Regiomontanus.

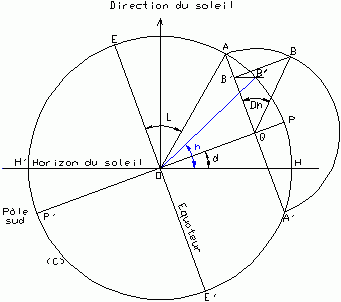Fig. 15

Du centre O traçons le cercle (C) du méridien de midi, il correspond à la circonférence de la terre
Par O traçons l'horizon du soleil HH'
Par O traçons l'axe des pôles PP' faisant avec l'horizon du soleil l'angle d de la déclinaison
Perpendiculairement à l'axe des pôles traçons l'équateur EE'
Traçons le rayon OA faisant avec l'équateur l'angle de la latitude L
Traçons parallèlement à l'équateur la corde AA' correspondante à la trace du parallèle
Du centre Q traçons le demi-cercle ABA' correspondant au rabattement du parallèle
Traçons le rayon QB faisant avec QA l'angle horaire terrestre Dh

Fig. 15

Abaissons B perpendiculairement à AA' pour obtenir la position de l'observateur B'
Reportons la distance de B' à l'horizon du soleil sur le cercle terrestre en traçant la droite B'B"
Traçons le rayon OB". L'angle de la hauteur du soleil correspond à HOB"

Pour tous les angles horaires terrestres correspondants à des heures entières traçons les parallèles à l'horizon du soleil et faisons tourner l'ensemble de 90°. Nous obtenons la figure 16 sur laquelle on peut associer:

Au point O le point de suspension du fil
Au point B" la perle coulissante
Aux différentes parallèles à l'horizon du soleil les lignes horaires rectilignes

Pour faire la démarche dans le sens inverse soit, à partir des lignes horaires rectilignes, retrouver le centre et le rayon de la terre, il faut, à partir du point Q situé sur la ligne centrale de 6 h:

Tracer, avec l'angle de la déclinaison et perpendiculairement entre eux, l'axe des pôles ainsi que la trace du parallèle QA, A étant situé sur la ligne horaire de 12 h
De A, avec l'angle de la latitude, tracer la droite AO donnant à la fois le centre O et le rayon OA

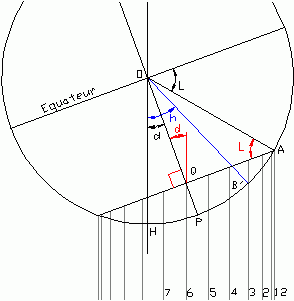Fig. 16

Le passage à l'Universel de Regiomontanus (Fig. 17) découle alors logiquement de cette procédure en la reproduisant pour plusieurs déclinaisons et latitudes. On remarquera alors, à l'image de ce que nous avons démontré avec le Capucin, que les points O se situent sur une droite perpendiculaire aux lignes horaires quand on fait varier la déclinaison pour une latitude donnée.

Fig. 17 Je tiens à remercier vivement Mrs S. Müller, J. Packomoff, J. Parès, D. Savoie, F. de Vries pour leurs réponses à mes multiples questions et les documents qu'ils m'ont généreusement fait parvenir.
Bibliographie:

Les cadrans solaires. Editions Belin-Pour la Science. Denis Savoie. 2003.
A "universal" Capucin Dial (or The Sailing Wooden Shoe). The Compendium Volume 6 Number 1. Fer J. de Vries. Mars 1999.
Universal Card Dials with Nomograms for Babylonian, Italian, and Antique Hours. The Compendium Volume 5 Number 4. Fer J. de Vries. Décembre 1998.
La gnomonique de Desargues à Pardiès. Jean Parès. Cahiers d’histoire et de philosophie des sciences n° 17. Editions Belin. 1988.
Les cadrans Solaires Rectilignes. Nuncius 3:2. Margarida Archinard. 1988.
Universal rectilinear Dials. The Mathematical Gazette. Vol 41. A. W. Fuller. Février 1957
Histoire de l’astronomie du moyen âge. J.-B. Delambre. 1819.
Récréations Mathématiques et Physiques. J. Ozanam. 1694.
Cursus mathematicus. Millet Deschalles. 1674
Instrument buch. P. Apian. 1533
Les "Calendriers" de Regiomontanus. A partir de 1474.

Fig. 17: L'Universel de Regiomontanus. Le fil doit être suspendu dans le trigone supérieur où on peut reconnaître les axes polaires. La perle se règle à l'extrémité du trigone latéral dont les rayons correspondent aux traces du parallèle où l'observateur se situe (gravure réalisée par les Prs Siegfried Müller et Harald Germer).

Sites personnels sur Internet:

Philippe Dutarte: http://perso.club-internet.fr/dutarte/Siteinstruments/REGIOMONTANUS.htm
Siegfried Müller: http://www.astro-ab.de/themen/uhrentafelchen/body_uhrentafelchen.htm
Jean Pakhomoff: http://membres.lycos.fr/pakhomoff/cap.html
Fer J. de Vries: http://www.dse.nl/~zonnewijzer/reg-cap.htm où se trouvent les deux articles du Compendium mentionnés ci-dessus

Retour à la page d'accueil

Date de création: 16 Juillet 2006


Fig. 2: L'Universel de Régiomontanus. Le fil est suspendu à l'intersection des lignes horizontales de latitude et des lignes inclinées de déclinaison. En tirant sur le fil, on règle la perle, ou ici le noeud, sur l'échelle latérale des déclinaisons.	Fig. 3: Le Capucin. Le point de suspension du fil se règle sur une échelle de date. La perle qui doit se régler sur le point 12 est remplacée ici par un ensemble d'arcs de cercle.

	La figure 4 montre la sphère céleste pour une latitude donnée telle qu'on a l'habitude de l'imaginer en gnomonique.
Fig. 4: La sphère céleste avec ses cercles horaires et de déclinaison

En projetant tous les cercles de la sphère perpendiculairement sur le plan du méridien on obtient la figure 5 encore appelée Analemme de Ptolémée. L'analemme doit être disposé en fonction de la latitude, puis, de la déclinaison et de l'heure solaire, on peut déterminer la position du soleil pour finalement déterminer sa hauteur au dessus de l'horizon.
	Fig. 5: L'analemme de Ptolémée. Le méridien devient le grand cercle principal, les cercles de déclinaison deviennent des segments de droite et les cercles horaires deviennent des portions d’ellipse.


Fig. 8	Fig. 9: Le capucin. On peut reconnaître dans l'échelle des dates l'axe des pôles, dans le point C le centre du cercle méridien, dans la longueur MC son rayon et dans le segment AM la trace du cercle de déclinaison (figure extraite du livre Les Cadrans Solaires de D. Savoie).
	En répétant l'opération précédente pour plusieurs latitudes, le passage à l'Universel d'Apian vient alors naturellement. Mais regardons d'abord sur la figure 8 ce qui se passe pour seulement 2 latitudes. Du point Q et pour la latitude L1, retrouvons le centre O1 du cercle méridien à l'aide du triangle QD1O1. De même pour la latitude L2 traçons le triangle QD2O2 pour obtenir le centre O2. Intéressons nous à présent au triangle QD1D2 et remarquons que: L'angle O1QO2 est égal à l'angle D1QD2 Les triangles QD1O1 et QD2O2 sont semblables donc QO1 est à QD1 ce que QO2 est à QD2 Par conséquent les triangles QD1D2 et QO1O2 sont donc semblables et comme la similitude est directe et d'angle droit, la droite O1O2 est donc perpendiculaire à la ligne de midi. Par extension, tous les centres O que nous obtiendrons pour des latitudes différentes mais pour la même déclinaison d seront situés sur cette droite. Nous pouvons à présent mieux comprendre la forme de l'Universel d'Apian présenté à la figure 10.
Fig. 10: L'Universel d’Apian. Le point de fixation du fil est dans le "papillon" supérieur à l'intersection des lignes inclinées de latitude (image des différents axes polaires) et des lignes horizontales de déclinaison. La perle se règle sur l'échelle latérale des latitudes (figure de Fer J. de Vries).

	Sur la figure 11, le pied du soleil est au Sénégal près de Dakar. Là, la hauteur du soleil est de 90°. Par Dakar passe le méridien vert, en tout lieu sur ce méridien il est midi vrai. 15° à l'ouest passe le méridien rouge, en tout lieu sur ce dernier il est 1 heure vraie.
Fig. 11: La terre éclairée par le soleil

Le cercle bleu appelé horizon du soleil sépare le monde de la lumière de celui des ténèbres. En tout lieu sur ce cercle, le soleil est vu sur l’horizon. Comme le montre la figure 12, en tout point du monde éclairé, l’angle de la hauteur du soleil correspond à l’angle, vu du centre de la terre, du lieu considéré au plan de l’horizon du soleil.
	Fig. 12: Vue en coupe de la terre. La coupe passe par le pied du soleil et le lieu considéré.

Représentons à présent, figure 13, la terre par tous ses cercles parallèles et méridiens. Ces derniers, régulièrement espacés tous les 15 °, peuvent être gradués en heure solaire comme nous l'avons vu ci-dessus. Convenons alors d'appeler angle horaire terrestre l'angle qui sépare un méridien donné du méridien de midi.
	Fig. 13: La terre avec tous ses parallèles et méridiens